Catagories

• Three broad categories
  • Descriptive
    • E.g. Observations, focus groups
    • Consider 8/10 who can play game and type fast
    • Interesting phenomena but not relationship

Catagories

• Three broad categories
  • Relational
    • E.g. Correlation Analysis
    • Consider hours played and words per minute
    • Relationship but not causality

Catagories

• Three broad categories
  • Experimental
    • E.g. Treatment Study
    • Consider a control and treatment
    • Causality can be established
• Types of studies are not totally independent

Catagories

Getting Started

• Start with a research hypothesis
  • Study built around this
  • Basis for statistical tests
• Theory vs Hypothesis
  • Theory: Fitts Law - Time increases as distance increases and target size decreases in movement tasks.
  • Hypothesis: Mouse, Touch, etc…

Hypothesis

• Null (\(H_0\)) vs Alternative (\(H_1\)) Hypothesis
  • Null hypothesis states that there is no difference between experimental treatments
  • Alternative hypothesis is mutually exclusive the null
• Some experiments have several

Hypothesis

• Experiment to determine which menu design allows users to navigate a site more effectively
  • \(H_0\): There is no difference between pull down and pop up menus in time spent locating pages.
  • \(H_1\): There is a difference between the pull down and pop up menus in time spent locating pages.
• Statistical test will tell us whether it is reasonable to reject the null hypothesis and the likelihood of being wrong

Testing Hypothesis

• You can test multiple hypothesis
• No limit but…
  • More factors to control for
  • Increased possibility of flaw

A Good Hypothesis

• A good hypothesis generally:
  • Is presented in clear, precise language
  • Is focused on a problem that is testable in a single experiment
  • Clearly states the control group or conditions of the experiment

Variables

• Different Types of Variables
  • Independent - What we are studying, changing, or might cause a change
    • Think treatments or conditions that researcher controls
    • E.g. Menu type

Variables

• Different Types of Variables
  • Dependant - The variables being measured that is dependent on participants behavior or change in the independent variable
    • Think outcomes
    • E.g. Time locating page
    • Some faster than others, more experienced, …

Independent Variables

• Typical Independent Variables
  • Devices
  • Modalities
  • Designs
  • User characteristics
    • Age, experience, mood, profession

Dependent Variables

• Dependent Variables usually one of 5 groups
  • Efficiency
  • Accuracy
  • Subjective Satisfaction
  • Learning/Retention
  • Physical/Cognitive Demand
• Efficiency and Accuracy are usually, but not always, related

Controlling Factors

• Experimental Research allows for controlling of factors
  • Randomized design
  • No one, including investigator, can predict which treatment group is used
  • Controls for intentional or subconscious influence of hidden factors

Controlling Factors

• Randomization measures
  • Tossing a coin
  • Throwing dice
  • Software, etc…
• Uniform Distribution Example - Histogram & Random Data

Design Types

• Consider comparing QWERTY to DVORAK
  • Need participants that have used neither or highly biased
  • Between-Subjects Design
    • Assign randomly to each group and measure
  • Within-Subjects Design
    • All participants use both and are measured
  • Mixed Factorial
    • Combination of both

Counterbalancing

• Measuring participant more than once?
  • Each participant does Task A, Task B, Task C
  • Several problems
    • Carryover effect
    • Fatigue effect
    • Context effect

Counterbalancing

• Measuring participant more than once?
  • Should counterbalance assigning order randomly
    • Consider using Latin Squares - ABC, ACB, BAC, BCA, CAB, CBA
    • Mitigates confounding ordering effects
    • Potentially allows for studying the problem ones, e.g. carryover

Significance Testing

• Nearly all experimental investigations use statistical significance testing
• Consider two statements:
  • Mike’s height is 6′2″. Mary’s height is 5′8″. So Mike is taller than Mary.
  • The average height of three males (Mike, John, and Ted) is 5′5″. The average height of three females (Mary, Rose, and Jessica) is 5′10″. So females are taller than males.
• Population vs Sample

Normal Distribution

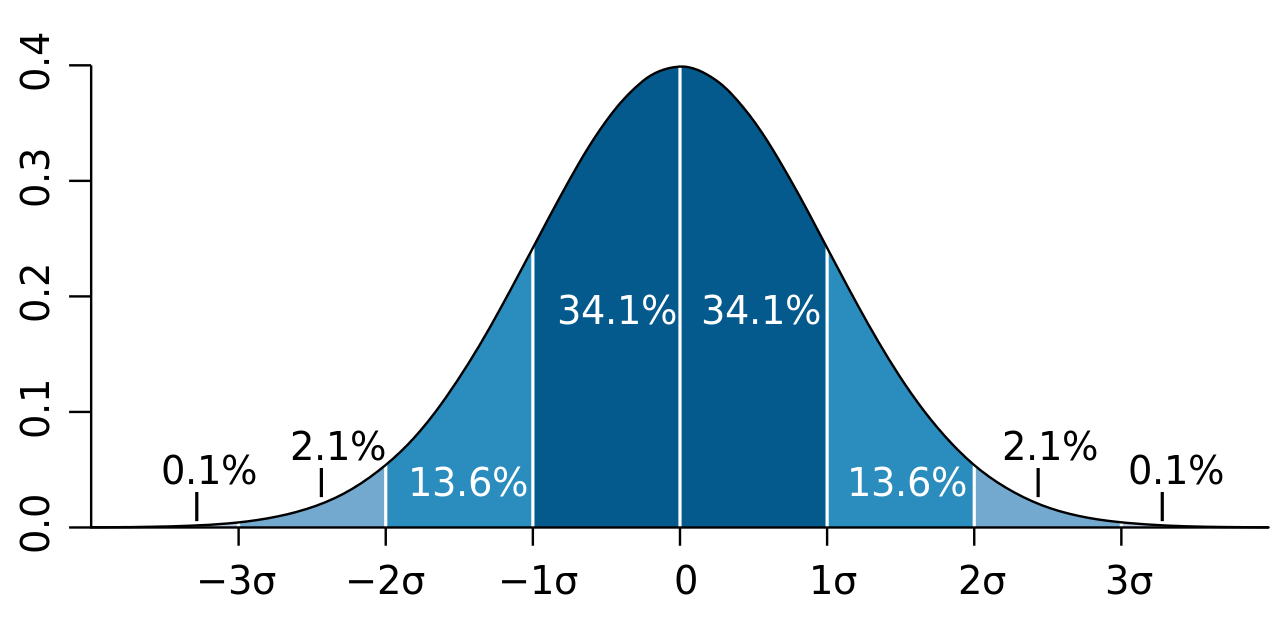
Significance Testing

• Use statistical test to help us be confident the result applies to the entire population
• For example, t-test with \(p < .05\) would indicate we are 95% certain the result applies to the general population
  • t-test calculator

Type I & II Errors

• Allows us to contrast \(H_0\) and \(H_1\) to determine the likelihood the null hypothesis (\(H_0\)) is true
• All significance testing is subject to Type I and Type II error
  • Type I - “false positive” or rejecting the null hypothesis when it should not be
  • Type II - “false negative” or accepting the null hypothesis when it should be rejected

Type I & II Errors

• Consider a court case where we presume the defendant is innocent
  • \(H_0\): The defendant is innocent
  • \(H_1\): The defendant is guilty
  • Both errors have very real costs

Type I & II Errors

Try It

• Consider a bank that wants to understand if ATMs with a touch screen are easier to use than ATMs with buttons
• In groups:
  • Identify the \(H_0\) and \(H_1\)
    • Identify Type I and II Errors

Try It

• Answer:
  • \(H_0\): There is no difference between the ease of use of ATMs with touch screens and ATMs with buttons.
  • \(H_1\): ATMs with touch screens are easier to use than ATMs with buttons.

Try It

Type I & II Errors

• Generally believed that Type I errors are worse than Type II
  • Type I is a mistake that involves “gullibility” and potentially results in a worse current state
  • Type II involves “blindness” and potentially loses ability to improve current state
• Consider medication study involving Type I and II errors

Type I & II Errors

• Type I is called alpha or significance level or p value
• Type II is called beta
• Alpha and beta are related, becoming less gullible means increased blindness
• \(p=.05\) is widely used

Hawthorne Effect

• Consider limitations e.g. “Hawthorne effect”
  • Short term improvements not lasting after observation
  • Incentive, stress, environment and so on

Experiments

• Experimental approaches are effective ways to generalize to larger populations
• Must be successfully designed and carried
• Must deal with potentially confounding variables
  • Random + increased sample size
  • Explicitly control for
  • Use as covariable

Questions

• Questions?